Géométrie analytique : Exercice 17 2ème année secondaire

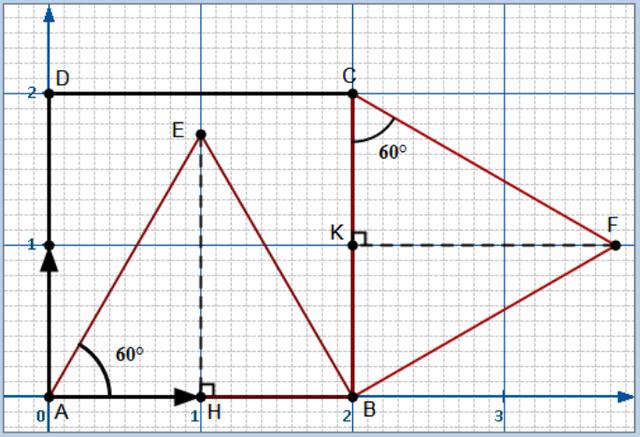
1 On considère le repère orthonormé $(A,\vec i,\vec j)$ où $\vec i=\dfrac{1}{2}\overrightarrow{AB}$ et $\vec j=\dfrac{1}{2}\overrightarrow{AD}$

• $\boxed{A(0;0)}$
• $\overrightarrow{AB}=2\left({\dfrac{1}{2}\overrightarrow{AB}}\right)=2\vec i\Longrightarrow \boxed{B(2;0)}$
• $\overrightarrow{AD}=2\left({\dfrac{1}{2}\overrightarrow{AD}}\right)=2\vec j\Longrightarrow \boxed{D(0;2)}$
• $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=2\vec i+ \vec j\Longrightarrow \boxed{C(2;2)}$
• Posons $H=A*B$, $EH=AE\times \sin\left({\dfrac{\pi}{3}}\right)=2\times \dfrac{\sqrt{3}}{2}=\sqrt{3}$ donc $\overrightarrow{AE}=\overrightarrow{AH}+\overrightarrow{HE}=\vec i+\sqrt{3}\vec j$ $\Longrightarrow \boxed{E(1;\sqrt{3})}$
• Posons $K=B*C$ , $KF=CF\times \sin\left({\dfrac{\pi}{3}}\right)=2\times \dfrac{\sqrt{3}}{2}=\sqrt{3}$ donc $\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BK}+\overrightarrow{KF}=2\vec i+\vec j+\sqrt{3}\vec i$ $=(2+\sqrt{3})\vec i+\vec j\Longrightarrow \boxed{F(2+\sqrt{3};1)}$

2 $M(x;y)\in (ED)$ $\iff \overrightarrow{DM}\left({\begin{aligned}&{x}\\&{y-2}\end{aligned}}\right)$ et $\overrightarrow{DE}\left({\begin{aligned}&{1}\\&{\sqrt{3}-2}\end{aligned}}\right)$ sont colinéaires $\iff \begin{vmatrix}{x}&{1}\\{y-2}&{\sqrt{3}-2}\end{vmatrix}=0$ $\iff (\sqrt{3}-2)x-(y-2)=0$ donc $\boxed{(ED): (\sqrt{3}-2)x-y+2=0}$

3 Vérifions que $F\in (DE)$
$F(2+\sqrt{3},1)$ , $(\sqrt{3}-2)(\sqrt{3}+2)-1+2=(3-4)-1+2=0$ $\Longrightarrow F\in (DE)$ d'où les points $D,E\; et \;F$ sont alignés