Trigonométrie : Exercice 13 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
24 exercices
Exercice 13 --- (id : 821)
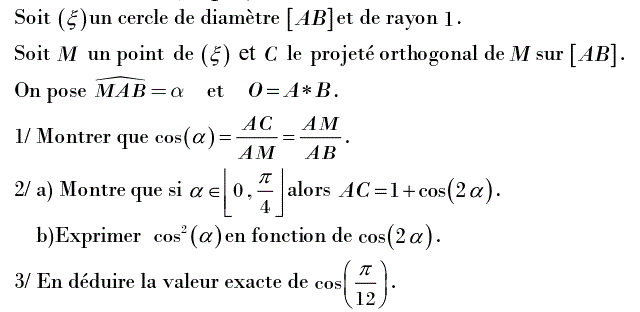
correction
1
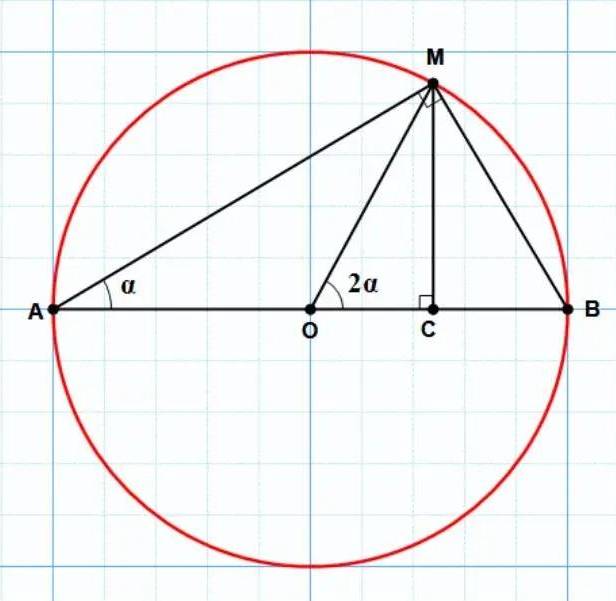
Le triangle $ACM$ est rectangle en $C$ donc $\cos \alpha=\dfrac{AC}{AM}$
$[AB]$ est un diamètre du cercle $𝒞$ et $M\in 𝒞$ donc le triangle $AMB$ est rectangle en $M$ donc $\cos \alpha=\dfrac{AM}{AB}$
Donc $\colorbox{SaddleBrown}{$\cos \alpha=\dfrac{AC}{AM}=\dfrac{AM}{AB}$}$
$[AB]$ est un diamètre du cercle $𝒞$ et $M\in 𝒞$ donc le triangle $AMB$ est rectangle en $M$ donc $\cos \alpha=\dfrac{AM}{AB}$
Donc $\colorbox{SaddleBrown}{$\cos \alpha=\dfrac{AC}{AM}=\dfrac{AM}{AB}$}$
2
a
Si $\alpha \in \left[{0;\dfrac{\pi}{4}}\right]$, alors $C\in \left[{OB}\right]$ et $AC=AO+OC=1+OC$
D'autre part l'angle $\widehat{MOB}$ est l'angle au centre associé à l'angle inscrit $\widehat{MAB}$ donc $\widehat{MOC}=\widehat{MOB}$ $=2\widehat{MAB}=2\alpha$ et $\cos 2\alpha=\dfrac{OC}{OM}=\dfrac{OC}{1}=OC$ et finalement $\colorbox{SaddleBrown}{$AC=1+OC=1+\cos 2\alpha$}$
D'autre part l'angle $\widehat{MOB}$ est l'angle au centre associé à l'angle inscrit $\widehat{MAB}$ donc $\widehat{MOC}=\widehat{MOB}$ $=2\widehat{MAB}=2\alpha$ et $\cos 2\alpha=\dfrac{OC}{OM}=\dfrac{OC}{1}=OC$ et finalement $\colorbox{SaddleBrown}{$AC=1+OC=1+\cos 2\alpha$}$
b
$\dfrac{AC}{AM}=\dfrac{AM}{AB}$ $\iff AM^2=AB.AC=2(1+\cos 2\alpha)$
$\cos \alpha=\dfrac{AM}{AB}$ $\iff AM^2=AB^2.\cos^2\alpha$ $=4\cos^2\alpha$
Donc $AM^2=AB.AC=2(1+\cos 2\alpha)=4\cos^2\alpha$ $\Longrightarrow \boxed{\cos^2\alpha=\dfrac{1+\cos 2\alpha}{2}}$
$\cos \alpha=\dfrac{AM}{AB}$ $\iff AM^2=AB^2.\cos^2\alpha$ $=4\cos^2\alpha$
Donc $AM^2=AB.AC=2(1+\cos 2\alpha)=4\cos^2\alpha$ $\Longrightarrow \boxed{\cos^2\alpha=\dfrac{1+\cos 2\alpha}{2}}$
3
Pour $\alpha=\dfrac{\pi}{12}$, $2\alpha=\dfrac{\pi}{6}$
on obtient alors $\cos^2\left({\dfrac{\pi}{12}}\right)=\dfrac{1+\cos\left({\dfrac{\pi}{6}}\right)}{2}$ $\iff \cos^2\left({\dfrac{\pi}{12}}\right)=\dfrac{1+\dfrac{\sqrt{3}}{2}}{2}$ $=\dfrac{2+\sqrt{3}}{4}$
$\Longrightarrow \boxed{\cos\left({\dfrac{\pi}{12}}\right)=\dfrac{\sqrt{2+\sqrt{3}}}{2}}$ car $\alpha=\dfrac{\pi}{12}\in \left[{0;\dfrac{\pi}{2}}\right]$ donc $\cos\left({\dfrac{\pi}{12}}\right)\geqslant 0$
Remarque
$\cos\left({\dfrac{\pi}{12}}\right)=\dfrac{\sqrt{2+\sqrt{3}}}{2}$ $=\dfrac{\sqrt{2}\sqrt{2+\sqrt{3}}}{2\sqrt{2}}$ $=\dfrac{\sqrt{4+2\sqrt{3}}}{2\sqrt{2}}$ $=\dfrac{\sqrt{(1+\sqrt{3})^2}}{2\sqrt{2}}$ $=\dfrac{1+\sqrt{3}}{2\sqrt{2}}=\dfrac{\sqrt{2}(1+\sqrt{3})}{\sqrt{2}(2\sqrt{2})}$ $=\dfrac{\sqrt{2}+\sqrt{6}}{4}$
$\colorbox{SaddleBrown}{$\cos\left({\dfrac{\pi}{12}}\right)=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{2}+\sqrt{6}}{4}$}$