Arithmetique : Exercice 9 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
56 exercices
Exercice 9 --- (id : 360)
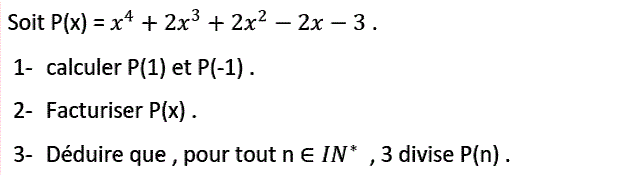
correction
$P(x)=x^4+2x^3+2x^2-2x-3$
1)
🔷$P(1)=1+2+2-2-3=0$
🔷$P(-1)=1-2+2+2-3=0$
🔷$P(1)=1+2+2-2-3=0$
🔷$P(-1)=1-2+2+2-3=0$
2)
$P(1)=0$ et $P(-1)=0$ donc $P(x)$ est factorisable par $x-1$ et $x+1$ donc pour tout réel x; $P(x)=(x-1)(x+1)Q(x)=(x^2-1)Q(x)$ où Q est un polynome de degré $2$
Alors cherchons les trois réels a, b et c tels que pour tout réel $x$ $P(x)=(x^2-1)(ax^2+bx+c)$
$$\begin{align*} \forall x \in \Bbb R&;\\ P(x)&=(x^2-1)(ax^2+bx+c) \\ &=ax^4+bx^3+cx^2-ax^2-bx-c \\ &=ax^4+bx^3+(c-a)x^2-bx-c \\ \iff\;\;& \left\{{\begin{aligned}&{a=1}\\&{b=2}\\&{c-a=2}\\&{-b=-2}\\ &{-c=-3}\end{aligned}}\right. \iff \left\{{\begin{aligned}&{a=1}\\&{b=2}\\&{c=3}\\&{c-a=3-1=2 \;vrai}\end{aligned}}\right. \end{align*}$$ Conclusion : $\forall x \in \Bbb R;P(x)=(x-1)(x+1)(x^2+2x+3)$
Alors cherchons les trois réels a, b et c tels que pour tout réel $x$ $P(x)=(x^2-1)(ax^2+bx+c)$
$$\begin{align*} \forall x \in \Bbb R&;\\ P(x)&=(x^2-1)(ax^2+bx+c) \\ &=ax^4+bx^3+cx^2-ax^2-bx-c \\ &=ax^4+bx^3+(c-a)x^2-bx-c \\ \iff\;\;& \left\{{\begin{aligned}&{a=1}\\&{b=2}\\&{c-a=2}\\&{-b=-2}\\ &{-c=-3}\end{aligned}}\right. \iff \left\{{\begin{aligned}&{a=1}\\&{b=2}\\&{c=3}\\&{c-a=3-1=2 \;vrai}\end{aligned}}\right. \end{align*}$$ Conclusion : $\forall x \in \Bbb R;P(x)=(x-1)(x+1)(x^2+2x+3)$
3)
En faisant la division euclidienne de $n$ par $3$, on obtient $n=3q+r$ où $q\in \Bbb N$ et $r\in \left\{{0;1;2}\right\}$
🔶Si $r=0$; $n=3q$ et $P(n)=(n-1)(n+1)(n^2+2n+3)$ $\iff P(n)=(3q-1)(3q+1)(9q^2+6q+3)$ $\iff P(n)=3(3q-1)(3q+1)3q^2+2q+1)$ donc $3$ divise $P(n)$
🔶Si $r=1$; $n=3q+1 \iff n-1=3q$ or $n-1$ divise $P(n)$ donc $3q$ divise $P(n)$ et par suite $3$ divise $P(n)$
🔶 Si $r=2$; $n=3q+2$ $\iff n+1=3q+3=3(q+1)=3q'$ or $n+1$ divise $P(n)$ donc $3q'$ divise $P(n)$ alors $3$ divise $P(n)$.
🔶Si $r=0$; $n=3q$ et $P(n)=(n-1)(n+1)(n^2+2n+3)$ $\iff P(n)=(3q-1)(3q+1)(9q^2+6q+3)$ $\iff P(n)=3(3q-1)(3q+1)3q^2+2q+1)$ donc $3$ divise $P(n)$
🔶Si $r=1$; $n=3q+1 \iff n-1=3q$ or $n-1$ divise $P(n)$ donc $3q$ divise $P(n)$ et par suite $3$ divise $P(n)$
🔶 Si $r=2$; $n=3q+2$ $\iff n+1=3q+3=3(q+1)=3q'$ or $n+1$ divise $P(n)$ donc $3q'$ divise $P(n)$ alors $3$ divise $P(n)$.