Equations et inéquations : Exercice 9 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
81 exercices
Exercice 9 --- (id : 1889)
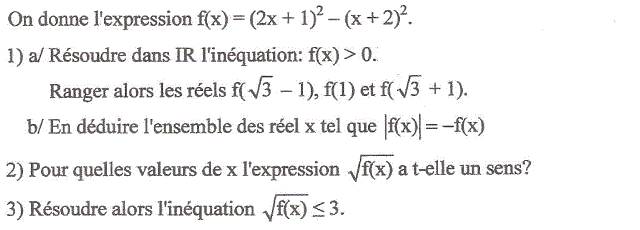
correction
1)
a-$f(x)>0$
$$\begin{equation*}
\begin{split}
\iff &(2x+1)^2-(x+2)^2>0 \\
\iff &4x^2+4x+1-x^2-4x-4>0 \\
\iff &3x^2-3>0 \\
\iff &3(x^2-1)>0 \\
\iff &x^2-1>0 \\
\iff & x\in \left]{-\infty,-1}\right[\cup\left]{1,+\infty}\right[
\end{split}
\end{equation*} $$
🔶 $f(x)=0 \iff x^2-1=0 \iff (x-1)(x+1)=0$ $\iff x-1=0$ ou $x+1=0$ $\iff x=1$ ou $x=-1$ donc $f(1)=f(-1)=0$
🔶 $0<\sqrt{3}-1<1$ donc $f(\sqrt{3}-1)< 0$
🔶 $\sqrt{3}+1>1$ donc $f(\sqrt{3}+1)>0$
Conclusion : $f(\sqrt{3}-1)<f(1)<f(\sqrt{3}+1)$
🔶 $0<\sqrt{3}-1<1$ donc $f(\sqrt{3}-1)< 0$
🔶 $\sqrt{3}+1>1$ donc $f(\sqrt{3}+1)>0$
Conclusion : $f(\sqrt{3}-1)<f(1)<f(\sqrt{3}+1)$
b-
$\left|{f(x)}\right|=-f(x)$ équivaut $f(x)\leqslant 0$ équivaut $x\in \left[{-1,1}\right]$
2)
$\sqrt{f(x)}$ existe $\iff f(x)\geqslant 0$ ou encore $f(x)>0$ ou $f(x)=0$
Donc $\sqrt{f(x)}$ existe si et seulement si $x \in \left]{-\infty,-1}\right]\cup\left[{1,+\infty}\right[$
Donc $\sqrt{f(x)}$ existe si et seulement si $x \in \left]{-\infty,-1}\right]\cup\left[{1,+\infty}\right[$
3)
Pour tout réel $x \in \left]{-\infty,-1}\right]\cup\left[{1,+\infty}\right[$ on a :
$\sqrt{f(x)}\leqslant 3$ $$\begin{equation*} \begin{split} \iff &f(x)\leqslant 9 \\ \iff &3x^2-3\leqslant 9 \\ \iff &3x^2\leqslant 12 \\ \iff &x^2\leqslant 4 \\ \iff &x^2-4\leqslant 0 \\ \iff &(x-2)(x+2)\leqslant 0 \\ \iff &x\in \left[{-2,2}\right] \end{split} \end{equation*} $$ $\sqrt{f(x)}\leqslant 3$ $\iff x\in \left[{-2,2}\right]\cap $ $\left({\left]{-\infty,-1}\right]\cup\left[{1,+\infty}\right[}\right)$ $\iff x\in \left[{-2,-1}\right]\cup \left[{1,2}\right]$
$\sqrt{f(x)}\leqslant 3$ $$\begin{equation*} \begin{split} \iff &f(x)\leqslant 9 \\ \iff &3x^2-3\leqslant 9 \\ \iff &3x^2\leqslant 12 \\ \iff &x^2\leqslant 4 \\ \iff &x^2-4\leqslant 0 \\ \iff &(x-2)(x+2)\leqslant 0 \\ \iff &x\in \left[{-2,2}\right] \end{split} \end{equation*} $$ $\sqrt{f(x)}\leqslant 3$ $\iff x\in \left[{-2,2}\right]\cap $ $\left({\left]{-\infty,-1}\right]\cup\left[{1,+\infty}\right[}\right)$ $\iff x\in \left[{-2,-1}\right]\cup \left[{1,2}\right]$