Trigonométrie : Exercice 2 2ème année secondaire

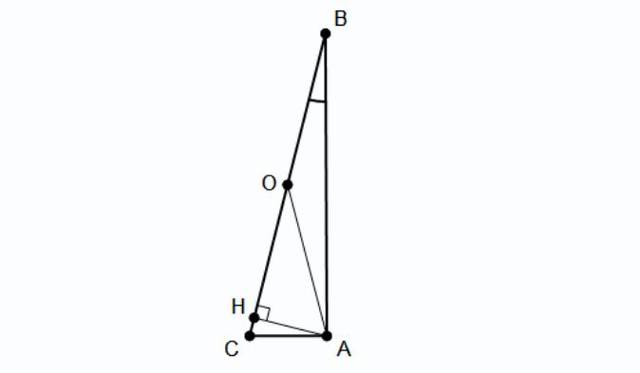
a Dans le cercle circonscrit au triangle $ABC$ (de diamètre [BC]) $\widehat{AOC}$ est l'angle au centre associé à l'angle inscrit $\widehat{ABC}$ donc $\widehat{AOH}=\widehat{AOC}=2\times\widehat{ABC}=2\times\dfrac{\pi}{12}=\dfrac{\pi}{6}$
Dans le triangle $AOH$, $\widehat{A}+\widehat{O}+\widehat{H}=\pi$ donc $\widehat{A}=\pi-\widehat{O}-\widehat{H}=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}$

b 🔹 $\cos\widehat{O}=\dfrac{OH}{OA}$ $\iff OH=OA\times\cos\widehat{O}$ $\iff OH=\dfrac{BC}{2}\times\cos\left({\dfrac{\pi}{6}}\right)$ $\iff OH=4\times \dfrac{\sqrt{3}}{2}=2\sqrt{3}$
🔹 Le triangle $AOH$ est rectangle en $H$ donc $AH^2=OA^2-OH^2$ $\iff AH=\sqrt{OA^2-OH^2}$ $\iff AH=\sqrt{16-12}=2$
🔹 Dans le triangle $AHB$ rectangle en $H$ on a: $HB=HO+OB=2\sqrt{3}+4$
$AB^2=HA^2+HB^2$
$\iff AB^2=4+(2\sqrt{3}+4)^2$
$\iff AB^2=4+12+16+16\sqrt{3}$
$\iff AB^2=32+16\sqrt{3}=16(2+\sqrt{3})$
$\iff AB=4\sqrt{2+\sqrt{3}}$

a Le triangle $AHB$ est rectangle en $H$ donc :
🔹 $\cos\widehat{B}=\dfrac{BH}{BA}$ $\iff \cos\widehat{B}=\dfrac{2\sqrt{3}+4}{4\sqrt{2+\sqrt{3}}}$ $\iff \boxed{\cos\left({\dfrac{\pi}{12}}\right)=\dfrac{\sqrt{2+\sqrt{3}}}{2}}$
🔹 $\sin\widehat{B}=\dfrac{AH}{AB}$ $\iff \sin\left({\dfrac{\pi}{12}}\right)=\dfrac{2}{4\sqrt{2+\sqrt{3}}}$ $\iff \sin\left({\dfrac{\pi}{12}}\right)=\dfrac{\sqrt{2-\sqrt{3}}}{2\sqrt{(2+\sqrt{3})(2-\sqrt{3})}}$ $\iff \boxed{\sin\left({\dfrac{\pi}{12}}\right)=\dfrac{\sqrt{2-\sqrt{3}}}{2}}$

b 🔹 $\cos\dfrac{5\pi}{12}=\cos\left({\dfrac{\pi}{2}-\dfrac{\pi}{12}}\right)$ $=\sin\dfrac{\pi}{12}=\dfrac{\sqrt{2-\sqrt{3}}}{2}$
🔹 $\sin\dfrac{5\pi}{12}=\sin\left({\dfrac{\pi}{2}-\dfrac{\pi}{12}}\right)$ $=\cos\dfrac{\pi}{12}=\dfrac{\sqrt{2+\sqrt{3}}}{2}$
🔹 $\cos\dfrac{11\pi}{12}=\cos\left({\pi-\dfrac{\pi}{12}}\right)$ $=-\cos\dfrac{\pi}{12}=-\dfrac{\sqrt{2+\sqrt{3}}}{2}$
🔹 $\sin\dfrac{11\pi}{12}=\sin\left({\pi-\dfrac{\pi}{12}}\right)$ $=\sin\dfrac{\pi}{12}=\dfrac{\sqrt{2-\sqrt{3}}}{2}$