Problèmes du 1er et du second degré : Exercice 4 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
115 exercices
Exercice 4 --- (id : 15)
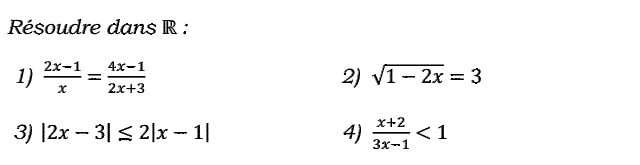
correction
1)
$\boxed{\frac{2x-1}{x}=\frac{4x-1}{2x+3}}$
Pour que x soit une solution de l'équation donnée il faut que : $x\neq 0\;et\; 2x+3\neq 0$ $\Leftrightarrow x\neq 0 \; et \; x\neq -\frac{3}{2}$
$\frac{2x-1}{x}=\frac{4x-1}{2x+3}$ $\Leftrightarrow (2x-1)(2x+3)=x(4x-1)$ $\Leftrightarrow 4x^2+6x-2x-3=4x^2-x$ $\Leftrightarrow 5x=3$ $\Leftrightarrow x=\frac{3}{5}$
Donc $\boxed{S_\Bbb R=\left\{{\frac{3}{5}}\right\}}$
Pour que x soit une solution de l'équation donnée il faut que : $x\neq 0\;et\; 2x+3\neq 0$ $\Leftrightarrow x\neq 0 \; et \; x\neq -\frac{3}{2}$
$\frac{2x-1}{x}=\frac{4x-1}{2x+3}$ $\Leftrightarrow (2x-1)(2x+3)=x(4x-1)$ $\Leftrightarrow 4x^2+6x-2x-3=4x^2-x$ $\Leftrightarrow 5x=3$ $\Leftrightarrow x=\frac{3}{5}$
Donc $\boxed{S_\Bbb R=\left\{{\frac{3}{5}}\right\}}$
2)
$\boxed{\sqrt{1-2x}=3}$
Pour que x soit une solution de cette équation il faut que x vérifie $1-2x\geqslant 0$ ou encore $x\leqslant \frac{1}{2}$
$\sqrt{1-2x}=3$ $\Leftrightarrow 1-2x=9\; et \; x\leqslant\frac{1}{2}$ $\Leftrightarrow -2x=8\; et \; x\leqslant\frac{1}{2}$ $\Leftrightarrow x=-4$
Donc $\boxed{S_\Bbb R=\left\{{-4}\right\}}$
Pour que x soit une solution de cette équation il faut que x vérifie $1-2x\geqslant 0$ ou encore $x\leqslant \frac{1}{2}$
$\sqrt{1-2x}=3$ $\Leftrightarrow 1-2x=9\; et \; x\leqslant\frac{1}{2}$ $\Leftrightarrow -2x=8\; et \; x\leqslant\frac{1}{2}$ $\Leftrightarrow x=-4$
Donc $\boxed{S_\Bbb R=\left\{{-4}\right\}}$
3)
$\boxed{|2x-3|\leqslant 2|x-1|}$
$2x-3=0\Leftrightarrow x=\frac{3}{2}$ et $x-1=0\Leftrightarrow x=1$
$$\def\arraystretch{1.5}\begin{array}{|c|ccccccc|} \hline x & -\infty & &1& &\frac{3}{2}& & +\infty \\ \hline |2x-3| & & -2x+3 & & -2x+3 & 0 & 2x-3 \\ \hline |x-1| & & -x+1 &0& x-1 & & x-1 \\ \hline \end{array}$$ 1er cas: $x\in \left]{-\infty,1}\right]$
$-2x+3\leqslant 2(-x+1)$ $\Leftrightarrow 3\leqslant 2$ ce qui est impossible
2ème cas: $x\in \left[{1,\dfrac{3}{2}}\right]$
$-2x+3\leqslant 2(x-1)$ $\Leftrightarrow -4x\leqslant -5$ $\Leftrightarrow x\geqslant \dfrac{5}{4}$ donc $x\in \left[{\dfrac{5}{4},\dfrac{3}{2}}\right]$
3ème cas: $x\in \left[{\dfrac{3}{2},+\infty}\right[$
$2x-3\leqslant 2(x-1)$ $\Leftrightarrow -3 \leqslant -2$ ce qui est vrai donc $x\in \left[{\dfrac{3}{2},+\infty}\right[$
Conclusion : $\boxed{S_\Bbb R=\left[{\dfrac{5}{4},+\infty}\right[}$
$2x-3=0\Leftrightarrow x=\frac{3}{2}$ et $x-1=0\Leftrightarrow x=1$
$$\def\arraystretch{1.5}\begin{array}{|c|ccccccc|} \hline x & -\infty & &1& &\frac{3}{2}& & +\infty \\ \hline |2x-3| & & -2x+3 & & -2x+3 & 0 & 2x-3 \\ \hline |x-1| & & -x+1 &0& x-1 & & x-1 \\ \hline \end{array}$$ 1er cas: $x\in \left]{-\infty,1}\right]$
$-2x+3\leqslant 2(-x+1)$ $\Leftrightarrow 3\leqslant 2$ ce qui est impossible
2ème cas: $x\in \left[{1,\dfrac{3}{2}}\right]$
$-2x+3\leqslant 2(x-1)$ $\Leftrightarrow -4x\leqslant -5$ $\Leftrightarrow x\geqslant \dfrac{5}{4}$ donc $x\in \left[{\dfrac{5}{4},\dfrac{3}{2}}\right]$
3ème cas: $x\in \left[{\dfrac{3}{2},+\infty}\right[$
$2x-3\leqslant 2(x-1)$ $\Leftrightarrow -3 \leqslant -2$ ce qui est vrai donc $x\in \left[{\dfrac{3}{2},+\infty}\right[$
Conclusion : $\boxed{S_\Bbb R=\left[{\dfrac{5}{4},+\infty}\right[}$
4)
$\boxed{\dfrac{x+2}{3x-1}<1}$
1er cas: $3x-1>0 \Leftrightarrow x>\frac{1}{3}$
$\dfrac{x+2}{3x-1}<1$ $\Leftrightarrow x+2<3x-1\;et\;x>\dfrac{1}{3}$ $\Leftrightarrow 2x>3\;et\;x>\dfrac{1}{3}$ $\Leftrightarrow x>\dfrac{3}{2}\;et\;x>\dfrac{1}{3}$ $\Leftrightarrow x>\dfrac{3}{2}$
2ème cas: $3x-1<0 \Leftrightarrow x<\frac{1}{3}$
$\dfrac{x+2}{3x-1}<1$ $\Leftrightarrow x+2>3x-1\;et\;x<\dfrac{1}{3}$ $\Leftrightarrow 2x<3\;et\;x<\dfrac{1}{3}$ $\Leftrightarrow x<\dfrac{3}{2}\;et\;x<\dfrac{1}{3}$ $\Leftrightarrow x<\dfrac{1}{3}$
Conclusion : $\boxed{S_\Bbb R=\left]{-\infty,\frac{1}{3}}\right[\cup\left]{\frac{3}{2},+\infty}\right[}$
1er cas: $3x-1>0 \Leftrightarrow x>\frac{1}{3}$
$\dfrac{x+2}{3x-1}<1$ $\Leftrightarrow x+2<3x-1\;et\;x>\dfrac{1}{3}$ $\Leftrightarrow 2x>3\;et\;x>\dfrac{1}{3}$ $\Leftrightarrow x>\dfrac{3}{2}\;et\;x>\dfrac{1}{3}$ $\Leftrightarrow x>\dfrac{3}{2}$
2ème cas: $3x-1<0 \Leftrightarrow x<\frac{1}{3}$
$\dfrac{x+2}{3x-1}<1$ $\Leftrightarrow x+2>3x-1\;et\;x<\dfrac{1}{3}$ $\Leftrightarrow 2x<3\;et\;x<\dfrac{1}{3}$ $\Leftrightarrow x<\dfrac{3}{2}\;et\;x<\dfrac{1}{3}$ $\Leftrightarrow x<\dfrac{1}{3}$
Conclusion : $\boxed{S_\Bbb R=\left]{-\infty,\frac{1}{3}}\right[\cup\left]{\frac{3}{2},+\infty}\right[}$