Généralités sur les fonctions : Exercice 2 3eme année secondaire
Généralités sur les fonctionsProduit scalaire dans le planLimites et continuitéAngles orientésDérivabilité
33 exercices
Exercice 2 --- (id : 4)
correction
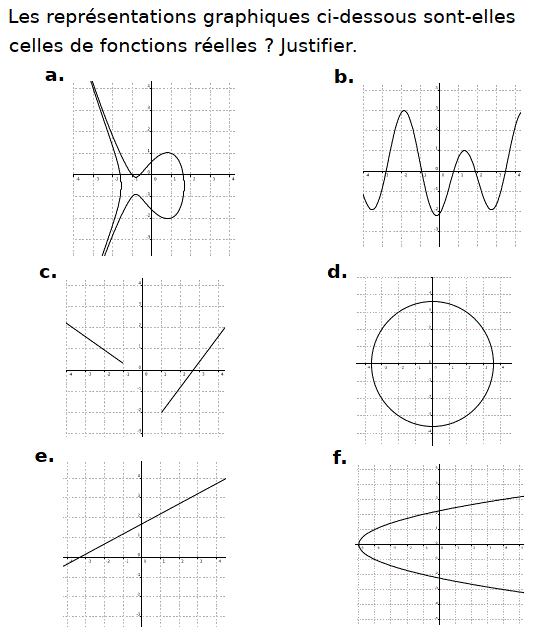
b. c. et e. sont des représentations graphiques de fonctions c-à-d des courbes cartésiennes
Pour les autres courbes ne représentent pas des fonctions à une seule variable réelle car un réel x peut avoir plus qu'une image donc la relation associée $x\longmapsto f(x)$ n'est pas une fonction
Pour les autres courbes ne représentent pas des fonctions à une seule variable réelle car un réel x peut avoir plus qu'une image donc la relation associée $x\longmapsto f(x)$ n'est pas une fonction