Calcul dans IR : Exercice 14 2ème année secondaire

Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM

78 exercices

Exercice 14 --- (id : 774)
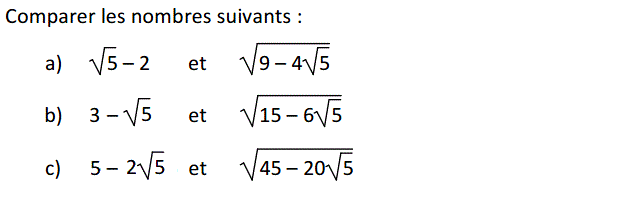
Calcul dans IR: Exercice 14
correction
a) (5−2)2(\sqrt 5-2)^2 =(5)2−2×5×2+22=(\sqrt 5)^2-2\times\sqrt5\times2+2^2 =5−45+4=5-4\sqrt 5+4 =9−45=9-4\sqrt 5
Donc 9−45\sqrt{9-4\sqrt 5} =(5−2)2=\sqrt{(\sqrt 5-2)^2} =∣5−2∣=5−2=|\sqrt 5-2|=\sqrt 5-2
b) (3−5)2(3-\sqrt5)^2 =32−2×3×5+(5)2=3^2-2\times3\times\sqrt5+(\sqrt5)^2 =9−65+5=14−65=9-6\sqrt5+5=14-6\sqrt5
0<14−65<15−650<14-6\sqrt5<15-6\sqrt5 donc 14−65<15−65\sqrt{14-6\sqrt5}<\sqrt{15-6\sqrt5}
Or 14−65=(3−5)2\sqrt{14-6\sqrt5}=\sqrt{(3-\sqrt5)^2} =∣3−5∣=3−5=|3-\sqrt5|=3-\sqrt5
D'où    3−5<15−653-\sqrt5<\sqrt{15-6\sqrt5}
c) 5−25=5(5−2)5-2\sqrt5=\sqrt5(\sqrt5-2) et 45−205=5(9−45)\sqrt{45-20\sqrt5}=\sqrt{5(9-4\sqrt5)} =59−45=\sqrt5\sqrt{9-4\sqrt5}
5−2=9−45\sqrt5-2=\sqrt{9-4\sqrt5}  donc   5−25=5(5−2)5-2\sqrt5=\sqrt5(\sqrt5-2) =59−45=\sqrt5\sqrt{9-4\sqrt5} =45−205=\sqrt{45-20\sqrt5}
<< < 1...5...91011121314 1516171819...24...34 > >>

Charte d'utilisation --- Plan du site
Copyright © 2010-2025 Dhaouadi Nejib - Tunisia