La fonction logarithme népérien
--- Dhaouadi Nejib ---
I.
Vue Historique
C’est à John NAPIER (ou NEPER), mathématicien écossais (1er février 1550 - 4 avril 1617), que l’on doit le mot et le concept de logarithme dans sa : « Description de la stupéfiante règle des logarithmes » en 1614.
Son but était la recherche d'une table de correspondance qui permette de simplifier les calculs en ramenant le calcul d’un produit à celui d'une somme. L‘introduction de cette technique de calcul allait conduire à des études théoriques qui permirent de dégager la notion de FONCTION LOGARITHME.
Son but était la recherche d'une table de correspondance qui permette de simplifier les calculs en ramenant le calcul d’un produit à celui d'une somme. L‘introduction de cette technique de calcul allait conduire à des études théoriques qui permirent de dégager la notion de FONCTION LOGARITHME.

Statue de John Napier, Galerie nationale écossaise des portraits
II.
Définition et propriétés1
Définition
Activité 1
On se propose de chercher les fonctions $f$ telles que :
- $f$ est définie et dérivable sur $\left]{0;+\infty}\right[$
- Pour tous nombres réels strictement positifs $a\;et\;b$, $f(ab)=f(a)+f(b)$
- On pose $a=1$ et $b=1$. Montrer que $f(1)=0$
- Soit $a>0$ fixé. On définie la fonction $g$ sur $\left]{0;+\infty}\right[$ par : $g(x)=f(ax)-f(x)$
- Vérifier que g est une fonction constante.
- Justifier que g est dérivable sur $\left]{0;+\infty}\right[$ et que pour tout réel $x>0\; g'(x)=af'(ax)-f'(x)$.
- En déduire que $g'(1)=af'(a)-f'(1)$
- On pose $f'(1)=k$ où $k\in\R$
Montrer alors que $f$ est la primitive sur $\left]{0;+\infty}\right[$ de la fonction $x\longmapsto \dfrac{k}{x}$ qui s'annule en $1$.
Pour $k=1$, la fonction $f$ est appelée fonction logarithme népérien.
☛ Définition
On appelle fonction logarithme népérien et on note $\ln$ l'unique primitive sur $\left]{0;+\infty}\right[$ de la fonction $x\longmapsto \dfrac{1}{x}$, qui s'annule en 1.
Conséquences
- La fonction $\ln$ est définie et dérivable sur $\left]{0;+\infty}\right[$ et $\forall x\in \left]{0;+\infty}\right[, \; \ln'(x)=\dfrac{1}{x}$
- $\ln(1)=0$
- La fonction $\ln$ est strictement croissante sur $\left]{0:+\infty}\right[$
- Pour tous réels strictement positifs $a\;et\;b$
$a<b \Longleftrightarrow \ln a<\ln b$ - Pour tous réels $a\;et\;b$ tels que $a>0 \;et\;b>0$
$a=b \Longleftrightarrow \ln a=\ln b$ - Pour tout réel strictement positif $a$
- $0<a<1\Longleftrightarrow\ln a< 0$
- $a>1\Longleftrightarrow\ln a> 0$
2
Propriétés
Activité 2
Soit $a>0$ et $f$ la fonction définie sur $\left]{0;+\infty}\right[$ par : $f(x)=\ln(ax)$.
- Montrer que $f$ est dérivable sur $\left]{0;+\infty}\right[$ et calculer $f'(x)$
- En déduire que pour tout $x\in \left]{0;+\infty}\right[; \ln(ax)=\ln x+\ln a$
Propriété fondamentale
Pour tous réels $a\;et\;b$ tels que $a>0 \;et\;b>0$
$\ln(ab)=\ln a+\ln b$
$\ln(ab)=\ln a+\ln b$
Activité 3
Soit $a$ et $b$ deux réels strictement positifs.
- En écrivant $a\times \dfrac{1}{a}=1$, montrer que $\ln\left({\dfrac{1}{a}}\right)=-\ln a$
- En écrivant $\dfrac{a}{b}=a\times \dfrac{1}{b}$, justifier que $\ln\left({\dfrac{a}{b}}\right)=\ln a-\ln b$
- Montrer, à l'aide d'un raisonnement par récurrence, que pour tout entier naturel n; $\ln(a^n)=n\ln a)$
- Déduire des questions précédentes que pour tout $n\in \Z_-;\;\; \ln(a^n)=n\ln a$
- Soit un entier $p\geqslant 2$. En écrivant $a=(\sqrt[p]{a})^p$, montrer que $\ln\left({\sqrt[p]{a}}\right)=\dfrac{1}{p}\ln a$
Propriétés
Pour tous réels strictement positifs $a$ et $b$.
$\ln\left({\dfrac{1}{a}}\right)=-\ln a$
$\ln\left({\dfrac{a}{b}}\right)=\ln a-\ln b$
$\ln\left({a^n}\right)=n\ln a\;\;$ ($n\in\Z$)
$\ln\left({\sqrt[p]{a}}\right)=\dfrac{1}{p}\ln a\;\;$ ($p\in \N,p\geqslant 2$)
$\ln\left({\dfrac{1}{a}}\right)=-\ln a$
$\ln\left({\dfrac{a}{b}}\right)=\ln a-\ln b$
$\ln\left({a^n}\right)=n\ln a\;\;$ ($n\in\Z$)
$\ln\left({\sqrt[p]{a}}\right)=\dfrac{1}{p}\ln a\;\;$ ($p\in \N,p\geqslant 2$)
📃 Exercice 1
- Résoudre dans $\R$ les équations suivantes:
$\ln(x^2+2x+2)=0$
$\ln(2x-1)=\ln x$ - Résoudre dans $\R$ les inéquations suivantes:
$\ln(x+2)>0$
$\ln(3x+1)<0$
$\ln(x^2+x+1)\geqslant \ln(x+2)$
Montrer les solutions
📃 Exercice 2
- Résoudre dans $\R$ l'équation
$\ln(x+1)+\ln(3-x)=\ln(4-x^2)$ - Résoudre dans $\R$ l'inéquation
$\ln(x+1)+\ln(3-x)<\ln(4-x^2)$
Montrer les solutions
📃 Exercice 3
- Calculer, sans utiliser la calculatrice, Chacun des nombres suivants:
- $A=\ln(\sqrt{5}-2)+\ln(\sqrt{5}+2)$
- $B=\ln 16+\ln 0.0625$
- $C=\ln \dfrac{6}{5}+\ln \dfrac{5}{3}$
- Exprimer en fonction de $\ln 3$ chacun des nombres suivants:
- $D=6\ln \sqrt{3}-\dfrac{1}{2}\ln 81$
- $E=\ln \dfrac{100}{9}+2\ln 2.7$
Montrer les solutions
Remarques
- Pour tous réels $a$ et $b$ tels que $ab\neq 0$ on a :
- $\ln\left|{ab}\right|=\ln \left|{a}\right|+\ln \left|{b}\right|$
- $\ln\left|{\dfrac{a}{b}}\right|=\ln \left|{a}\right|-\ln \left|{b}\right|$
- En particulier si $ab>0$ on a :
- $\ln\left({ab}\right)=\ln \left|{a}\right|+\ln \left|{b}\right|$
- $\ln\left({\dfrac{a}{b}}\right)=\ln \left|{a}\right|-\ln \left|{b}\right|$
- Pour tout entier pair $n$ et pour tout réel $a\neq 0$ on a :
- $\ln\left({a^{n}}\right)=n\ln\left|{a}\right|$
Exemples ✍
Pour tout réel $x\in \left]{-\infty;-1}\right[\cup \left]{1;+\infty}\right[$ $\ln(x^2-1)$ existe et on a :
$\ln(x^2-1)=\begin{cases} \ln(x-1)+\ln(x+1) &\text{si } {\;x\in\left]{1;+\infty}\right[} \\ \ln(1-x)+\ln(-x-1) &\text{si}{\;x\in\left]{-\infty;-1}\right[} \end{cases}$
Pour tout réel $x\neq 0$ $\ln(x^2)=\begin{cases} 2\ln x &\text{si} {\;x>0} \\ 2\ln(-x) &\text{si}{\; x<0} \end{cases}$
$\ln(x^2-1)=\begin{cases} \ln(x-1)+\ln(x+1) &\text{si } {\;x\in\left]{1;+\infty}\right[} \\ \ln(1-x)+\ln(-x-1) &\text{si}{\;x\in\left]{-\infty;-1}\right[} \end{cases}$
Pour tout réel $x\neq 0$ $\ln(x^2)=\begin{cases} 2\ln x &\text{si} {\;x>0} \\ 2\ln(-x) &\text{si}{\; x<0} \end{cases}$
III.
Etude et représentation Graphique de la fonction ln Activité 1
On se propose de déterminer la limite de la fonction $\ln$ en $+\infty$.
Soit $A$ un réel strictement positif.
Soit $A$ un réel strictement positif.
- Montrer que $\lim\limits_{n \to +\infty}\ln 2^n=+\infty$
- En déduire qu'il existe un entier naturel $n_0$ tel que $\ln 2^{n_0}>A$
- Montrer alors qu'il existe un réel $B>0$ tel que pour tout réel $x$, $x>B\Longrightarrow \ln x>A$
- Conclure.
Montrer les solutions
Activité 2
- Montrer que $\lim\limits_{x \to 0^+}\ln x=-\infty$
- Monter que pour tout réel $t\geqslant 1\;,\dfrac{1}{t}\leqslant \dfrac{1}{\sqrt{t}}$.
En déduire que $\ln x\leqslant 2\sqrt{x}-2$ pour $x\geqslant 1$ - Montrer alors que $\lim\limits_{x \to +\infty}\dfrac{\ln x}{x}=0$ et déterminer $\lim\limits_{x \to 0^+}x\ln x$
- Monter que pour tout réel $t\geqslant 1\;,\dfrac{1}{t}\leqslant \dfrac{1}{\sqrt{t}}$.
- Montrer que $\lim\limits_{x \to 1}\dfrac{\ln x}{x-1}=1$ et déduire $\lim\limits_{x \to 0}\dfrac{\ln(1+x)}{x}$
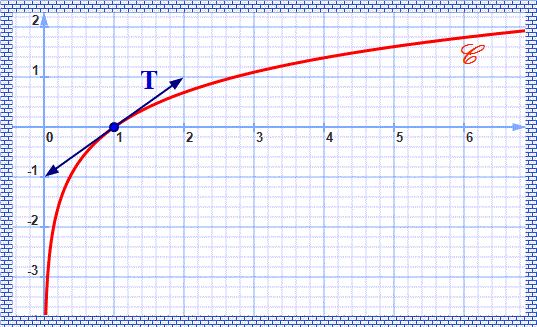
- On note $𝒞$ la courbe représentative de la fonction $\ln$
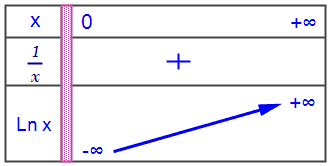
- Dresser le tableau de variation de la fonction $\ln$
- Ecrire une équation de la tangente T à la courbe $𝒞$ au point d'abscisse 1.
- Construire la courbe $𝒞$ dans un repère orthonormé $(O,\vec i,\vec j)$
Montrer les solutions
☛ Retenons
$\lim\limits_{x \to +\infty}\ln x=+\infty$ ; $\lim\limits_{x \to 0^+}\ln x=-\infty$ ;
$\lim\limits_{x \to +\infty}\dfrac{\ln x}{x}=0$ ; $\lim\limits_{x \to 0^+}x\ln x=0$ ; $\lim\limits_{x \to 1}\dfrac{\ln x}{x-1}=1$ ; $\lim\limits_{x \to 0}\dfrac{\ln(1+x)}{x}=1$
Remarques
- La fonction $\ln$ est continue et strictement croissante sur $\left]{0;+\infty}\right[$ donc elle réalise une bijection de $\left]{0;+\infty}\right[$ sur $\ln\left({ \left]{0;+\infty}\right[}\right)=\R$.
- L'unique solution de l'équation $\ln x=1$ est notée $e$ (cette notation a été donnée par le mathématicien EULER qui a démontré aussi que $e$ n'est pas un nombre rationnel.) .
- $e$ est appelé la base de la fonction logarithme népérien. Une valeur approchée de $e$ est : $2,718281828456$
Activité 3
On désigne par (C) la courbe représentative de la fonction ln dans un repère orthonormé.
Soit A un point de (C) d’abscisse a, la tangente à (C) en A coupe l’axe des ordonnées en I. On désigne par H le projeté orthogonal de A sur l’axe des ordonnées et par $y_H$ et $y_I$ les ordonnées respectives des points H et I.
Soit A un point de (C) d’abscisse a, la tangente à (C) en A coupe l’axe des ordonnées en I. On désigne par H le projeté orthogonal de A sur l’axe des ordonnées et par $y_H$ et $y_I$ les ordonnées respectives des points H et I.
- Montrer que $y_H — y_I$ est constant.
- En déduire une construction de la tangente en un point de la courbe (C).
Construction de la tangente
- La courbe $(𝒞)$ est la représentation graphique de la fonction $\ln$.
- $M(x,y)$ est un point de la courbe $(𝒞)$
- $H$ le projeté orthogonal de $M$ sur l'axe des ordonnées
- $(\Gamma)$ le cercle de centre $H$ et de rayon 1
- $(Γ)$ coupe l'axe des ordonnées en un point $I$ tel que $y_I < y_H$.
- La tangente à la courbe $(𝒞)$ en $M$ est la droite $(MI)$
IV.
Autres limites Activité 4
Soit $m$ un entier naturel non nul et $n$ un entier supérieur à 2.
- Vérifier que $\dfrac{\left({\ln x}\right)^n}{x^m}=\left({\dfrac{n} {m}\times \dfrac{\ln \left({\sqrt[n]{x^m}}\right)}{\sqrt[n]{x^m}}}\right)^n,\quad x>0$
- En déduire que $\lim\limits_{x \to +\infty}\dfrac{\left({\ln x}\right)^n}{x^m}=0$
- Calculer $\lim\limits_{x \to 0^+}\left|{x^m \left({\ln x}\right)^n}\right|$
Montrer les solutions
☛ Théorème
Pour tous entiers naturels non nuls $n$ et $m$ on a :
$\lim\limits_{x \to +\infty}\dfrac{\left({\ln x}\right)^n}{x^m}=0$ et $\lim\limits_{x \to 0^+}x^m \left({\ln x}\right)^n=0$
$\lim\limits_{x \to +\infty}\dfrac{\left({\ln x}\right)^n}{x^m}=0$ et $\lim\limits_{x \to 0^+}x^m \left({\ln x}\right)^n=0$
📃 Exercice 4
Calculer les limites suivantes :
$\lim\limits_{x \to +\infty} x-\ln x$ ; $\lim\limits_{x \to +\infty}\dfrac{\ln(2x)}{x^2+1}$ ; $\lim\limits_{x \to +\infty} 2\left({\ln x}\right)^2-7\ln x +3$ ; $\lim\limits_{x \to +\infty}\dfrac{\ln(3x)-1}{\ln(2x)+1}$ ; $\lim\limits_{x \to +\infty}\dfrac{\left({1+\ln x}\right)^2}{1+x}$
$\lim\limits_{x \to +\infty} x-\ln x$ ; $\lim\limits_{x \to +\infty}\dfrac{\ln(2x)}{x^2+1}$ ; $\lim\limits_{x \to +\infty} 2\left({\ln x}\right)^2-7\ln x +3$ ; $\lim\limits_{x \to +\infty}\dfrac{\ln(3x)-1}{\ln(2x)+1}$ ; $\lim\limits_{x \to +\infty}\dfrac{\left({1+\ln x}\right)^2}{1+x}$
Montrer les solutions
📃 Exercice 5
Calculer les limites suivantes :
$\lim\limits_{x \to +\infty}x\ln\left({1+\dfrac{1}{x}}\right)$ ; $\lim\limits_{x \to 0}\dfrac{\ln(1+3x)}{x}$ ; $\lim\limits_{x \to 3}\dfrac{\ln(x-2)}{x-3}$ ; $\lim\limits_{x \to 0}\dfrac{\ln\left({x^2+x+1}\right)}{x}$ ; $\lim\limits_{x \to 1^-}(x-1)\ln |x^2-1|$
$\lim\limits_{x \to +\infty}x\ln\left({1+\dfrac{1}{x}}\right)$ ; $\lim\limits_{x \to 0}\dfrac{\ln(1+3x)}{x}$ ; $\lim\limits_{x \to 3}\dfrac{\ln(x-2)}{x-3}$ ; $\lim\limits_{x \to 0}\dfrac{\ln\left({x^2+x+1}\right)}{x}$ ; $\lim\limits_{x \to 1^-}(x-1)\ln |x^2-1|$
Montrer les solutions
V.
Fonctions x⟼ln(u(x)) et x⟼ ln(|u(x)|) Activité 5
Soit $u$ une fonction dérivable sur un intervalle $I$ et vérifiant $\forall x \in I; u(x)>0$
Montrer, en utilisant le théorème de la dérivabilité de la composée, que la fonction $f$ définie sur $I$ par : $f(x)=\ln(u(x))$ est dérivable sur $I$ et pour tout $x \in I, f'(x)=\dfrac{u'(x)}{u(x)}$
Montrer, en utilisant le théorème de la dérivabilité de la composée, que la fonction $f$ définie sur $I$ par : $f(x)=\ln(u(x))$ est dérivable sur $I$ et pour tout $x \in I, f'(x)=\dfrac{u'(x)}{u(x)}$
Montrer les solutions
☛ Théorème
Soit $u$ une fonction dérivable sur un intervalle $I$ et telle $\forall x\in I, u(x)>0$
Alors la fonction $f$ définie sur $I$ par : $f(x)=\ln(u(x))$ est dérivable sur $I$ et $\forall x\in I, f'(x)=\dfrac{u'(x)}{u(x)}$
Alors la fonction $f$ définie sur $I$ par : $f(x)=\ln(u(x))$ est dérivable sur $I$ et $\forall x\in I, f'(x)=\dfrac{u'(x)}{u(x)}$
Activité 6
Soit $u$ une fonction dérivable sur un intervalle $I$ et vérifiant $\forall x \in I; u(x)\neq 0$
Montrer que la fonction $f$ définie sur $I$ par : $f(x)=\ln|u(x)|$ est dérivable sur $I$ et calculer $f'(x)$.
Montrer que la fonction $f$ définie sur $I$ par : $f(x)=\ln|u(x)|$ est dérivable sur $I$ et calculer $f'(x)$.
Montrer les solutions
Corollaire
Soit $u$ une fonction dérivable sur un intervalle $I$ et telle que $u(x)\neq 0$ pour tout $x\in I$
Alors la fonction $f:x\longmapsto \dfrac{u'(x)}{u(x)}$ admet comme primitive sur $I$ la fonction $F:x\longmapsto \ln(\left|{u(x)}\right|)+k$ où k est une constante réelle.
Alors la fonction $f:x\longmapsto \dfrac{u'(x)}{u(x)}$ admet comme primitive sur $I$ la fonction $F:x\longmapsto \ln(\left|{u(x)}\right|)+k$ où k est une constante réelle.
📃 Exercice 6
Dans chacun des cas suivants, déterminer le domaine de définition de $f$, étudier la dérivabilité et calculer $f'(x)$.
- $f(x)=\ln\left({\dfrac{x-1}{x+1}}\right)$
- $f(x)=\ln\left({\sqrt{4-x^2}}\right)$
- $f(x)=\ln\left|{\tan(x)}\right|$
Montrer les solutions
📃 Exercice 7
Dans chacun des cas suivants déterminer une primitive $F$ de la fonction $f$ sur l'intervalle $I$.
- $f(x)=\dfrac{1}{2x-1}$; $I=\left]{\dfrac{1}{2};+\infty}\right[$
- $f(x)=\dfrac{x^2}{x^3-1}$; $I=\left]{1;+\infty}\right[$
- $f(x)=\dfrac{x^2+x+1}{x^2+1}\;;I=R$
Montrer les solutions
📃 Exercice 8
On pose $g(x)=\ln\left|{\tan\left({\dfrac{x}{2}}\right)}\right|$
- Déterminer le domaine de définition $D_g$ de g.
- Montrer que g est dérivable sur $D_g$ et calculer $g'(x)$
- Déterminer la primitive $F$ de la fonction $f:x\longmapsto \dfrac{1}{\sin x}$sur l'intervalle $\left[{\dfrac{\pi}{6};\dfrac{5\pi}{6}}\right]$ qui s'annule en $\dfrac{\pi}{3}$.
Montrer les solutions
Activité
Soit la fonction $u:x\longmapsto x\ln x$
Calculer $u'(x)$.
En déduire une primitive de la fonction $\ln$.
Calculer $u'(x)$.
En déduire une primitive de la fonction $\ln$.
Montrer les solutions
☛ Théorème
Une primitive de la fonction $\ln$ sur $\left]{0;+\infty}\right[$ est la fonction $x\longmapsto x\ln x-x$
VI.
Exercices 📃 Exercice 9
Simplifier les sommes suivantes :
- $\ln\left({1+\sqrt{3}}\right)+\ln\left({\sqrt{3}-1}\right)$.
- $\ln\left({2+\sqrt{3}}\right)+\ln\left({2-\sqrt{3}}\right)$.
- $\ln 2+\ln\left({2+\sqrt{2}}\right)+\ln\left({2+\sqrt{2+\sqrt{2}}}\right)+\ln\left({2-\sqrt{2+\sqrt{2}}}\right)$.
📃 Exercice 10
- Calculer la limite de la fonction $f$ en $+\infty$ dans chacun des cas suivants :
$f(x)=\dfrac{\ln x}{\sqrt{x}}$ ; $f(x)=x^2-x+1-2\ln x$ ; $f(x)=x\ln x-3x^3$ ; $f(x)=\dfrac{\ln(1+x^2)}{x^2}$ ; $f(x)=\dfrac{\ln(x^2+x+1)}{x\dfrac{}{}}$ - Calculer la limite de la fonction $f$ à droite en 0 dans chacun des cas suivants :
$f(x)=\dfrac{\ln x-2}{\ln x-1}$ ; $f(x)=\dfrac{\ln(1+x)}{x^2}$ ; $f(x)=\dfrac{\ln(1-x)}{\ln x}$ ; $f(x)=\dfrac{1}{x}\ln\left({\dfrac{1-x}{1+x}}\right)$
📃 Exercice 11
Dans chacun des cas suivants, déterminer la dérivée de $f$ sur $D$.
- $f(x)=2x\ln x-3x$ et $D=\left]{0;+\infty}\right[$
- $f(x)=\dfrac{\ln x}{x}$ et $D=\left]{0;+\infty}\right[$
- $f(x)=\ln(x^2+x+1)$ et $D=\R$
- $f(x)=\ln\left({\dfrac{3-x}{3+x}}\right)$ et $D=\left]{-3;3}\right[$
- $f(x)=\ln\left|{3x-2}\right|$ et $D=\R╲\left\{{\dfrac{2}{3}}\right\}$
- $f(x)=x\ln\left|{\dfrac{5+x}{5-x}}\right|$ et $D=\R╲\left\{{-5;5}\right\}$
📃 Exercice 12
Dans chacun des cas suivants, déterminer la primitive de $f$ sur $I$ qui prend la valeur $y_0$ en $x_0$.
- $f(x)=\dfrac{5}{3-2x}$ ; $I=\left]{\dfrac{3}{2};+\infty}\right[$ ; $x_0=2$ et $y_0=-3$
- $f(x)=\dfrac{1}{x\ln x}$ ; $I=\left]{1;+\infty}\right[$ ; $x_0=e^2$ et $y_0=2\ln 2$
- $f(x)=\dfrac{\ln x}{x}$ ; $I=\left]{0;+\infty}\right[$ ; $x_0=e$ et $y_0=\dfrac{3}{2}$.
📃 Exercice 13
On considère la fonction $f$ définie sur $I=\left]{1;+\infty}\right[$ par :$f(x)=\dfrac{-3x^2+17x-4}{3x^2-4x+1}$
- Déterminer trois nombres réels $a,b\;et \;c$ tels que : pour tout x élément de $I$, $f(x)=a+\dfrac{b}{1-3x}-\dfrac{c}{1-x}$
- Déduire alors la primitive de $f$ sur $I$ qui prend la valeur $\dfrac{\ln 25}{3}$ en 2.
📃 Exercice 14
Soit $f$ la fonction définie sur $\R_+$ par : $f(x)=\dfrac{x^2}{2}\left({\ln x-\dfrac{3}{2}}\right)\;si\;x>0$ et $f(0)=0$.
On note $𝒞$ la courbe représentative de $f$ dans le plan muni d'un repère orthonormé $(O,I,J)$.
On note $𝒞$ la courbe représentative de $f$ dans le plan muni d'un repère orthonormé $(O,I,J)$.
- Etudier la continuité et la dérivabilité de $f$ à droite en 0.
- Calculer la limite de $f$ en $+\infty$.
- Vérifier que : $\forall x\in \left]{0;+\infty}\right[,f'(x)=x(\ln x-1)$
- Dresser le tableau de variations de $f$.
- Donner une équation de la tangente $T$ à la courbe $𝒞$ au point d'abscisse 1.
- Tracer $T$ et $𝒞$ dans le repère $(O,I,J)$.
📃 Exercice 15
On considère la fonction $f$ définie sur l'intervalle $\left[{0;+\infty}\right[$ par : $f(x)=\dfrac{1}{2}x^2\ln x-\dfrac{3}{4}x^2\;\;si\;x>0$ et $f(0)=0$.
On désigne par $𝒞$ la courbe représentative de $f$ dans le plan muni d'un repère orthonormé $(O,\vec i,\vec j)$.
On désigne par $𝒞$ la courbe représentative de $f$ dans le plan muni d'un repère orthonormé $(O,\vec i,\vec j)$.
- Etudier la continuité et la dérivabilité de $f$ à droite en 0.
- Déterminer la limite de $\dfrac{f(x)}{x}$ quand $x$ tend vers $+\infty$.
- Interpréter graphiquement les résultats précédents.
- Justifier que pour tout $x>0,\;f'(x)=x(\ln x-1).$
- Etudier les variations de $f$ et dresser son tableau de variations.
- Déterminer les points d'intersection de la courbe $𝒞$ et l'axe des abscisses.
- Déterminer une équation de la tangente $T$ à la courbe $𝒞$ au point d'abscisse 1.
- Construire $T$ et $𝒞$ dans le repère $(O,\vec i,\vec j)$.
📃 Exercice 16
$f$ est la fonction définie sur $I=\left]{0;+\infty}\right[$ par :
$f(x)=x-4+\ln\left({\dfrac{x}{x+1}}\right)$
$f(x)=x-4+\ln\left({\dfrac{x}{x+1}}\right)$
- Démontrer que $f$ est strictement croissante sur $I$.
- Démontrer que la droite (D) d'équation $y=x-4$ est une asymptote à la courbe représentative $𝒞$ de $f$ au voisinage de $+\infty$
- Préciser la position de $𝒞$ par rapport à (D)
- Construire (D) puis $𝒞$
📃 Exercice 17
A. Etude d'une fonction auxiliaire
Soit $g$ la fonction définie sur $\left[{\left[{0;+\infty}\right[}\right[$ par : $g(x)=\dfrac{2x^2}{x^2+1}-\ln(1+x^2)$- Démontrer que sur l'intervalle $\left[{1;+\infty}\right[$, l'équation $g(x)=0$ admet une solution unique $\alpha$ et donner un encadrement d'amplitude $10^{-1}$.
- Préciser le signe de $g$ sur l'intervalle $\left[{0;+\infty}\right[$.
B.Etude d'une fonction
$f$ est la fonction définie sur $I=\left[{0;+\infty}\right[$ par : \begin{cases} f(x)=\dfrac{\ln(1+x^2)}{x} &\text{si} {\;x>0} \\ f(0)=0 \end{cases}- Montrer que $f$ est dérivable à droite en 0 et donner une équation de la demi tangente à la courbe $𝒞$ représentation graphique de $f$.
- Vérifier que pour tout $x>0$, $f(x)=\dfrac{2\ln x}{x}+\dfrac{1}{x}\ln\left({1+\dfrac{1}{x^2}}\right)$
- En déduire la limite de $f$ en $+\infty$.
- Démontrer que pour tout réel $x>0,\;f'(x)=\dfrac{g(x)}{x^2}$
- Etudier les variations de $f$ et drésser son tableau de variations.
- Construire $T$, puis $𝒞$
📃 Exercice 18
$f$ et $g$ sont deux fonctions définies sur $\left[{1;+\infty}\right[$ par :
$f(x)=\ln\left({\dfrac{x+1}{x}}\right)-\dfrac{1}{x}$ et $g(x)=\ln\left({\dfrac{x+1}{x}}\right)-\dfrac{1}{x+1}$
$f(x)=\ln\left({\dfrac{x+1}{x}}\right)-\dfrac{1}{x}$ et $g(x)=\ln\left({\dfrac{x+1}{x}}\right)-\dfrac{1}{x+1}$
- Etudier les variations de $f$ et $g$.
- En déduire que pour tout réel $x\geqslant 1$,
$\dfrac{1}{x+1}\leqslant \ln(x+1)-\ln x\leqslant \dfrac{1}{x}$ (1)
- On note $(V_n)$ la suite définie pour tout entier $n\geqslant 1$ par : $V_n=1+\dfrac{1}{2}+...+\dfrac{1}{n}$
- En utilisant la relation (1), démontrer que : $V_n\geqslant \ln(n+1)$
- En déduire que $\lim\limits_{n \to +\infty}V_n=+\infty$
📃 Exercice 19
$f$ est la fonction définie sur $\left]{0;+\infty}\right[$ par : $f(x)=x+\ln x$ et $𝒞$ sa courbe représentative dans un repère orthonormé $(O,\vec i,\vec j)$.
- Etudier les variations de $f$ et tracer sa courbe $𝒞$
- Démontrer que pour tout entier naturel $n$, l'équation $f(x)=n$ admet une unique solution $\alpha_n$ dans $\left]{0;+\infty}\right[$
- Démontrer que la suite $(\alpha_n)$ est strictement croissante.
- $A$ est le point de $𝒞$ d'anscisse 1.
- Déterminer une équation de la tangente $\Delta$ à $𝒞$ en $A$.
- Démontrer que la courbe $𝒞$ est en dessous de la droite $\Delta$
- Exploiter les résultats de la question précédente pour démontrer que pour tout entier naturel $n$ non nul, $\dfrac{n+1}{2}\leqslant \alpha_n$
- Déterminer la limite de la suite $(\alpha_n)$
📃 Exercice 20
Soit $(u_n)$ la suite réelle définie sur $\N^*$ par : $u_n=\left({1+\dfrac{1}{n^2}}\right)\left({1+\dfrac{2}{n^2}}\right)...\left({1+\dfrac{n}{n^2}}\right)$
- En étudiant les variations de deux fonctions convenablement choisies, démontrer que pour tout réel $x\geqslant 0$, on a : $x-\dfrac{x^2}{2}\leqslant \ln(1+x)\leqslant x$.
- Démontrer par récurrence que pour tout entier $n\geqslant 1$, $\sum\limits_{k=1}^{n}{k^2}=\dfrac{n(n+1)(2n+1)}{6}$.
- Utiliser alors les résultats des questions précédentes pour trouver la limite de la suite $(u_n)$
📃 Exercice 21
$f$ est la fonction définie sur $\left]{0;+\infty}\right[$ par : $f(x)=\dfrac{\ln x}{x}$. On note $f^{(n)}$ la dérivée n-ième de $f$ avec $n\geqslant 1$.
- Calculer pour tout réel $x>0$, $f^{(1)}(x)$ et $f^{(2)}(x)$.
- Démontrer par récurrence que pour tout entier naturel $n\geqslant 1$ : $f^{(n)}(x)=\dfrac{u_n+v_n\ln x}{x^{n+1}}$ pour tout réel $x>0$ avec : $\left\{{\begin{aligned}&{u_1=1\;,\;v_1=-1}\\&{u_{n+1}=v_n-(n+1)u_n}\\&{v_{n+1}=-(n+1)v_n}\end{aligned}}\right.$
- Exprimer $v_n$ en fonction de $n$.
- Démontrer par récurrence que : $u_n=(-1)^{n+1}n!\left({1+\dfrac{1}{2}+...+\dfrac{1}{n}}\right)$.
- En déduire $f^{(7)}(x).$
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Connectez vous pour ajouter des commentaires.