Système de Lindenmayer et les plantes fractales
Dhaouadi Nejib
Le système de Lindenmayer
Lindenmayer (1925-1989) est un biologiste hongrois qui a proposé en 1968 une méthode pour décrire la structuration des plantes. Il a inventé un modèle de développement que l’on appelle maintenant L-System (ou système de Lindenmayer). Ce système est un ensemble de règles et de symboles qui permettent de modéliser la croissance d'un objet. Ce modèle s’applique également à la suite de Fibonacci, au flocon de Koch, puis à la forme des arbres ou des feuilles. Un L-Système permet de modéliser entièrement le développement et la croissance d’un système arborescent.
Les symbols les plus utilisés sont les suivants:
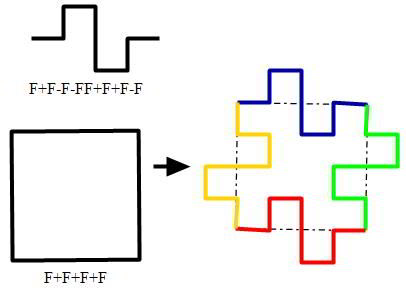
Et puis une règle de réécriture ou de remplacement: F --> F+F-F-FF+F+F-F
Après une seule itération, on obtient la chaine suivante sans parenthèses:
(F+F-F-FF+F+F-F) + (F+F-F-FF+F+F-F) + (F+F-F-FF+F+F-F) + (F+F-F-FF+F+F-F)
La deuxième itération nous donne la chaine suivante:
F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F

Les symbols les plus utilisés sont les suivants:
- F : Se déplacer d’un pas unitaire.
- + : Tourner à gauche d’angle α.
- - : Tourner à droite d’un angle α.
- [ : Sauvegarder la position courante.
- ] : Restaurer la dernière position sauvée.
Exemple
Considérons une chaine de caractères initiale (appelée axiome): F+F+F+FEt puis une règle de réécriture ou de remplacement: F --> F+F-F-FF+F+F-F
Après une seule itération, on obtient la chaine suivante sans parenthèses:
(F+F-F-FF+F+F-F) + (F+F-F-FF+F+F-F) + (F+F-F-FF+F+F-F) + (F+F-F-FF+F+F-F)

La deuxième itération nous donne la chaine suivante:
F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F

Les plantes fractales
A l'aide du système de Lindenmayer, vous pouvez utiliser un logiciel convenable pour tracer des plantes fractales, il suffit de faire un recherche sur google pour trouver des logiciels utilisant le L-system pour tracer des fractales.
Ici j'utilise mon propre logiciel que j'ai conçu moi même pour tracer des exemples de fractales.
Dans chaque exemple, on donne l'axiome, les règles et l'image générée.
Ici j'utilise mon propre logiciel que j'ai conçu moi même pour tracer des exemples de fractales.
Dans chaque exemple, on donne l'axiome, les règles et l'image générée.
Axiome : F Règle : F --> F[+F]F[-F][F] Angle = 24° n=4 et n=6

Axiome : F Règle : F --> F[+F]F[-F] Angle = 22° n=4 et n=6

Axiome : F Règle : F --> F[+F-F]F[-F] Angle = 22° n=4 et n=6

Axiome : F Règle : F --> [-F+F]FF[+FF] Angle = 24° n=4 et n=6
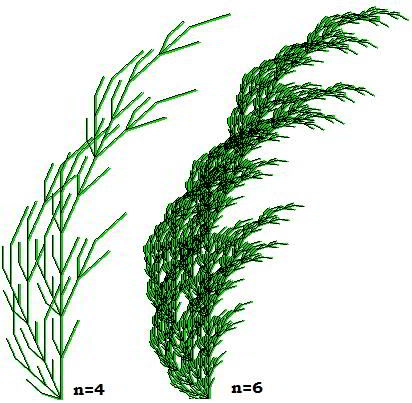
Axiome : F Règle : F --> FF-[-F+F]+[+F-F] Angle = 24° n=4 et n=6

Axiome : F Règle : F --> FF-[-F+F+F]+[+F-F-F] Angle = 24° n=4 et n=5

Axiome : F Règle : F --> FF[+FF][-FF] Angle = 18° n=4 et n=6
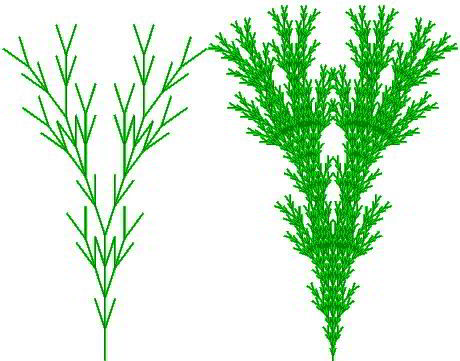
Axiome : X Règles : X --> F-[[X]+X]+F[+FX]-X F --> FF Angle = 20° n=4 et n=7

Axiome : Y Règles : X --> X[-FF][+FF]FX Y --> YFX[+YY][-YY] Angle = 25,7° n=4 et n=6
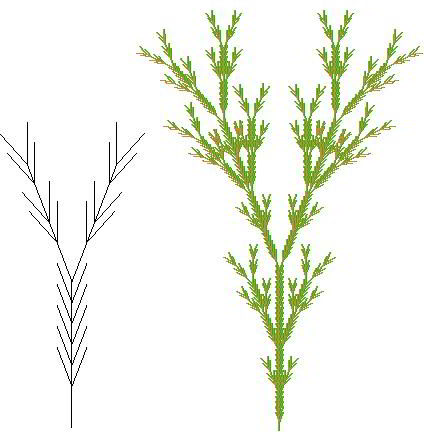
axiome : VZFFF Regles: V -> [+++W][---W]YV
W -> +X[-W]Z
X -> -W[+X]Z
Y -> YZ
Z -> [-FFF][+FFF]F
angle = 20°

Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Connectez vous pour ajouter des commentaires.