Questions mathématiques diverses
SigMathS
Question 86:Soit $ABC$ un triangle tel que $\widehat{A}=\dfrac{\pi}{7}$, $\widehat{B}=\dfrac{2\pi}{7}$ et $\widehat{C}=\dfrac{4\pi}{7}$
On pose $BC=a,\,AC=b$ et $AB=c$
Exprimer $a^2+b^2+c^2$ en fonction du rayon $R$ du cercle circonscrit au triangle $ABC$
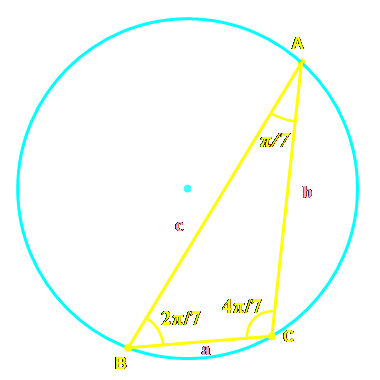
Soit $ABC$ un triangle tel que $\widehat{A}=\dfrac{\pi}{7}$, $\widehat{B}=\dfrac{2\pi}{7}$ et $\widehat{C}=\dfrac{4\pi}{7}$
On pose $BC=a,\,AC=b$ et $AB=c$
Exprimer $a^2+b^2+c^2$ en fonction du rayon $R$ du cercle circonscrit au triangle $ABC$

SigMathS
Réponse 86:Théorème des sinus
$\dfrac{a}{\sin \widehat{A}}=\dfrac{b}{\sin \widehat{B}}=\dfrac{c}{\sin \widehat{C}}=2R$
$$\begin{align*} &\sin^2 \widehat{A}+\sin^2\widehat{B}+\sin^2\widehat{C}\\ =&\sin^2 \dfrac{\pi}{7}+\sin^2\dfrac{2\pi}{7}+\sin^2\dfrac{4\pi}{7}\\ =&\dfrac{1-\cos \frac{2\pi}{7}}{2}+\dfrac{1-\cos \frac{4\pi}{7}}{2}+\dfrac{1-\cos \frac{8\pi}{7}}{2}\\ =&\dfrac{3-(\cos\frac{2\pi}{7}+\cos\frac{4\pi}{7}+\cos\frac{8\pi}{7})}{2}\\ =&\dfrac{3-(\cos\frac{2\pi}{7}+\cos\frac{4\pi}{7}+\cos\frac{6\pi}{7})}{2}\\ \end{align*}$$ les racines 7ème de l'unité sont de la forme $z_k=e^{i\frac{2k\pi}{7}}$ où $k\in\left\{{0,1,2,3,4,5,6}\right\}$ donc $\sum\limits_{k=0}^{6}{z_k}=0$ ce qui donne $1+\cos \frac{2\pi}{7}+\cos \frac{4\pi}{7}+\cos \frac{6\pi}{7}\\ \qquad +\cos \frac{8\pi}{7}+\cos \frac{10\pi}{7}+\cos \frac{12\pi}{7}=0\\ \iff 1+\cos \frac{2\pi}{7}+\cos \frac{4\pi}{7}+\cos \frac{6\pi}{7}\\ \qquad +\cos \frac{6\pi}{7}+\cos \frac{4\pi}{7}+\cos \frac{2\pi}{7}=0\\ \iff 2(\cos \frac{2\pi}{7}+\cos \frac{4\pi}{7}+\cos \frac{6\pi}{7})=-1\\ \iff \cos \frac{2\pi}{7}+\cos \frac{4\pi}{7}+\cos \frac{6\pi}{7}=-\dfrac{1}{2}$
$a^2+b^2+c^2=4R^2\dfrac{3-\left({-\dfrac{1}{2}}\right)}{2}$ $\iff \boxed{a^2+b^2+c^2=7R^2}$