Suites : Exercice 5 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
86 exercices
Exercice 5 --- (id : 608)
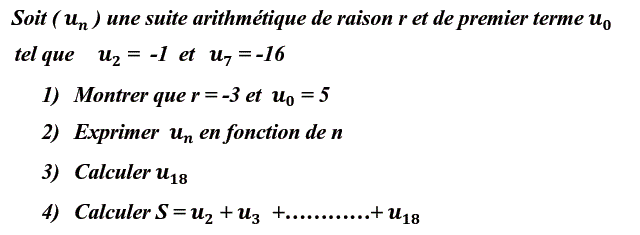
correction
Rappel : Si $(u_n)$ est une suite arithmétique de raison r et de premier terme $u_0$ alors :
🔶Pour tout entier $n$; $u_n=u_0+nr$
🔶Pour tout entiers naturels $p$ et $q$ : $u_p=u_q+(p-q)r$
🔶Pour tout entiers naturels $n$ et $m$ tels que : $n\leqslant m$; $\sum\limits_{k=n}^{m}{u_k}=\dfrac{m-n+1}{2}\left({u_n+u_m}\right)$
🔶Pour tout entier $n$; $u_n=u_0+nr$
🔶Pour tout entiers naturels $p$ et $q$ : $u_p=u_q+(p-q)r$
🔶Pour tout entiers naturels $n$ et $m$ tels que : $n\leqslant m$; $\sum\limits_{k=n}^{m}{u_k}=\dfrac{m-n+1}{2}\left({u_n+u_m}\right)$
1
$u_7=u_2+(7-2)r$ $\iff r=\dfrac{u_7-u_2}{7-2}$ $\iff r=\dfrac{-16-(-1)}{5}$ $\iff \boxed{r=-3}$
$u_2=u_0+2r$ $\iff u_0=u_2-2r \iff \boxed{u_0=-1-2(-3)=5}$
$u_2=u_0+2r$ $\iff u_0=u_2-2r \iff \boxed{u_0=-1-2(-3)=5}$
2
Pour tout entier naturel n; $u_n=u_0+nr$ $\iff \boxed{u_n=5-3n}$
3
$u_{18}=5-3\times18=-49$
4
$S=u_2+u_3+...+u_{18}$ $\iff S=\sum\limits_{k=2}^{18}{u_k}$ $\iff S=\dfrac{18-2+1}{2}\left({u_2+u_{18}}\right)$ $\iff S=\dfrac{17}{2}(-1-49)=-425$